Summary
Investigated is the effect of a surface irregularity on the propagation of waves in an isotropic, elastic plate, the method of perturbation being employed to determine the scattered field to the first order in a small parameter descriptive of the height of the irregularity. While the firstorder displacement field in the region under, and in the immediate vicinity of, the disturbed surface is very complicated, the far field in either direction, generated by either a symmetric or an antisymmetric incident wave, consists of a finite number of propagating waves, symmetric and antisymmetric, their number corresponding to the number of real roots of the frequency equation for the given frequency of incident wave.
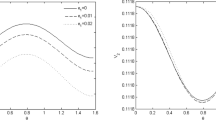
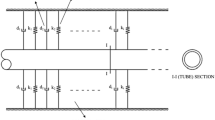
The general, analytical, results are then applied to the example of a plate having a small triangular protrusion or indentation on one of its surfaces, and the displacement is displayed in graphical form.
In the course of the investigation it is shown that the roots of the Rayleigh-Lamb frequency equation are symmetrically located about the axes of the reals and imaginaries.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
H. Deresiewicz andB. Wolf,The effect of boundaries on wave propagation in a liquid-filled porous solid: VIII. Reflection of plane waves at an irregular boundary, Bull. Seismol. Soc. Am.54 (1964), 1537–1561.
I. K. McIvor,Two-dimensional scattering of a plane compressional wave by surface imperfections, Bull. Seismol. Soc. Am.59 (1969), 1349–1364.
B. Wolf andH. Deresiewicz,On mapping an irregular boundary by means of reflected-wave measurements, Pure and Appl. Geophys.72 (1969/I), 13–16.
G. H. Handelman,Surface waves over a slightly curved elastic half-space, Prager Anniversary Volume (Macmillan, 1963), pp. 43–54.
M. K. Paul,The propagation of surface waves in elastic mediums with slightly curved boundaries of sinusoidal type, Pure and Appl. Geophys.62 (1965/III), 105–117.
S. Asano,Reflection and refraction of elastic waves at a corrugated interface, Bull. Seismol. Soc. Am.56 (1966), 201–221.
A. Levy andH. Deresiewicz,Reflection and transmission of elastic waves in a system of corrugated layers, Bull. Seismol. Soc. Am.57 (1967), 393–419.
B. Wolf,Propagation of Love waves in surface layers of varying thickness, Pure and Appl. Geophys.67 (1967/II), 76–82.
B. Wolf,Propagation of Love waves in layers with irregular boundaries, Pure and Appl. Geophys.78 (1970/I), 48–57.
L. M. Slavin andB. Wolf,Scattering of Love waves in a surface layer with an irregular boundary for the case of a rigid underlaying half-space, Bull. Seismol. Soc. Am.60 (1970), 859–877.
I. A. Viktorov,Rayleigh and Lamb Waves (Plenum, 1967).
K. Dransfeld andE. Salzmann,Excitation, detection, and attenuation of high-frequency elastic surface waves, inPhysical Acoustics, Vol. VII, W. P. Mason and R. N. Thurston, eds. (Academic Press, 1970), pp. 219–272.
Lord Rayleigh,On the free vibrations of an infinite plate of homogeneous isotropic elastic matter, Proc. London Math. Soc.20 (1888–1889), 225–234.
H. Lamb,On waves in an elastic plate, Proc. Royal Soc. London (A)93 (1917), 114–128 In the introductory paragraph of this paper reference is made to earlier work on two-dimensional waves in a solid bounded by parallel planes, by Lord Rayleigh (our reference [13]) and by the author (On the flexure of an elastic plate, Proc. London Math. Soc.21 (1889–1890), p. 85), but examination of the latter reveals only a further reference to his work, unpublished because of the prior appearance of Rayleigh's paper.
R. D. Mindlin Waves and vibrations in isotropic, elastic plates, inStructural Mechanics, J. N. Goodier and N. J. Hoff, eds. (Pergamon, 1960), pp. 199–232.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Sumner, J.H., Deresiewicz, H. Waves in an elastic plate with an irregular boundary. PAGEOPH 96, 106–126 (1972). https://doi.org/10.1007/BF00875633
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00875633