Abstract
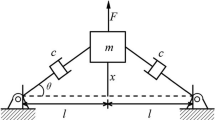
An approximate solution of the problem of the forced, geometrically nonlinear vibrations of an arbitrary viscoelastic body is found in the form of an expansion in eigenfunctions of the corresponding linear elastic problem. With the aid of the virtual displacement principle the problem is reduced to a system of nonlinear integro-differential equations whose periodic solution is constructed by the small-parameter method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
A. I. Lur'e Theory of Elasticity [in Russian], Moscow (1970).
A. N. Filatov, Averaging in Differential and Integro-Differential Equations [in Russian], Tashkent (1971).
I. G. Malkin, The Methods of Lyapunov and Poincare in the Theory of Nonlinear Oscillations [in Russian], Moscow-Leningrad (1949).
Additional information
Moscow Institute of Electronic Machine Building. Translated from Mekhanika Polimerov, No. 4, pp. 689–694, July–August, 1974.
Rights and permissions
About this article
Cite this article
Kravchuk, A.S., Morgunov, B.I. & Troyanovskii, I.E. Forced nonlinear vibrations of a viscoelastic body. Polymer Mechanics 10, 589–593 (1974). https://doi.org/10.1007/BF00855454
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00855454