Skip to main content
SpringerLink
Log in

“Minimax length links” of a dissimilarity matrix and minimum spanning trees

  • Published:
Psychometrika Aims and scope Submit manuscript

Abstract

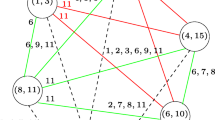
A theorem is proved stating that the set of all “minimax links”, defined as links minimizing, over paths, the maximum length of links in any path connecting a pair of objects comprising nodes in an undirected weighted graph, comprise the union of all minimum spanning trees of that graph. This theorem is related to methods of fitting network models to dissimilarity data, particularly a method called “Pathfinder” due to Schvaneveldt and his colleagues, as well as to single linkage clustering, and results concerning the relationship between minimum spanning trees and single linkage hierarchical trees.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Dearholt, D. W., & Schvaneveldt, R. W. (1990). Properties of Pathfinder networks. In R. W. Schvaneveldt (Ed.),Pathfinder associative networks: Studies in knowledge organization (pp. 1–30). Norwood, NJ: Ablex.

    Google Scholar 

  • Gower, J. C., & Ross, G. J. S. (1969). Minimum spanning trees and single linkage cluster analysis.Applied Statistics, 18, 54–64.

    Google Scholar 

  • Hartigan, J. A. (1975).Clustering algorithms. New York: John Wiley & Sons.

    Google Scholar 

  • Hutchinson, J. W. (1981). Network representations of psychological relations. Unpublished doctoral dissertation, Stanford University.

  • Hutchinson, J. W. (1989). NETSCAL: A network scaling algorithm for non-symmetric proximity data.Psychometrika, 54, 25–52.

    Google Scholar 

  • Johnson, S. C. (1967). Hierarchical clustering schemes.Psychometrika, 32, 241–254.

    Google Scholar 

  • Klauer, K. C. (1989). Ordinal representation: Representing proximities by graphs.Psychometrika, 54, 737–750.

    Google Scholar 

  • Klauer, K. C., & Carroll, J. D. (1989). A mathematical programming approach to fitting general graphs.Journal of Classification, 6, 247–270.

    Google Scholar 

  • Klauer, K. C., & Carroll, J. D. (1991). A comparison of two approaches to fitting directed graphs to nonsymmetric proximity measures.Journal of Classification, 8, 251–268.

    Google Scholar 

  • Kruskal, J. B. (1956). On the shortest spanning subtree of a graph and the traveling salesman problem.Proceedings of the American Mathematical Society, 7, 48–50.

    Google Scholar 

  • Prim, R. C. (1957). Shortest connection networks and some generalizations.The Bell System Technical Journal, XXXVI, 1389–1401.

    Google Scholar 

  • Schvaneveldt, R. W., Dearholt, D. W., & Durso, F. T. (1988). Graph theoretic foundations of Pathfinder networks.Comput. Math. Applic., 15, 337–345.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Management, Rutgers University, 181 New Street, 07102-1895, Newark, NJ

    J. Douglas Carroll

Authors
  1. J. Douglas Carroll
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Acknowledgments: The author thanks Phipps Arabie, Lawrence J. Hubert, and K. Christoph Klauer for a number of helpful suggestions and comments on various aspects of this paper.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Carroll, J.D. “Minimax length links” of a dissimilarity matrix and minimum spanning trees. Psychometrika 60, 371–374 (1995). https://doi.org/10.1007/BF02294381

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02294381

Key words

Search

Navigation