Abstract
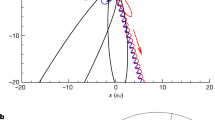
KIRKWOOD GAPS1 are gaps in the distribution of mean motion of asteroids at the multiples 2/1, 5/2, 3/1 and so on, of Jupiter's mean motion; but at the value 3/2, there is actually a concentration. Figure 1 shows the distribution of the best-determined orbits in the (semi-major axis, eccentricity)- or (a, e)-plane around the 2/1 resonance (the Hecuba Gap) and the 3/2 resonance (the Hilda Group). The sharp contrast between the two cases, especially in the eccentricity range 0.15<e<0.25, demonstrates the problem, and I show here that the Hilda region is stable in a well-defined sense, and the Hecuba region is unstable.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout
Similar content being viewed by others
References
Kirkwood, D. Smithsonian Inst. A. Rep.(1868).
Schubart, J. Smithsonian Inst. Res. Space Sci. Spec. Rep. No. 149 (1964).
Poincaré, H. Bull. Astr. 19, 189–310 (1902).
Brown, E. W. & Shook, A. C. Planetary Theory ch. 8 (Dover, New York, 1933).
Giffen, R. Astr. Astrophys. 23, 387–403 (1973).
Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste 1, ch. 4 (Gauthier–Villars, Paris, 1892).
Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste 3, 141 (Gauthier–Villars, Paris, 1892).
Kiang, T. Mon. Not. R. astr. Soc. 162, 271–287 (1973).
Hill, G. W. Acta. Math. 8, 1–36 (1886).
Schubart, J. Astr. J. 73, 99–103 (1968).
Franklin, F. A., Marsden, B. G., Williams, J. G. & Bardwell, C. M. Astr. J. 80, 729–746 (1975).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
KIANG, T. Kirkwood Gaps and stability of conservative periodic systems. Nature 273, 734–736 (1978). https://doi.org/10.1038/273734a0
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/273734a0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.