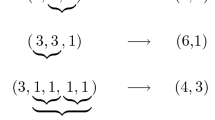
Abstract
Using a new graphical representation for partitions, the author obtains a family of partition identities associated with partitions into distinct parts of an arithmetic progression, or, more generally, with partitions into distinct parts of a set that is a finite union of arithmetic progressions associated with a modular sum-free Sidon set. Partition identities are also constructed for sets associated with modular sum-free sets.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
K. Alladi, “A variation on a theme of Sylvester-a smoother road to Göllnitz' theorem,” Discrete Math. 196 (1999) 1–11.
P.A. MacMahon, “The theory of modular partitions,” Proc. Cambridge Philos. Soc. 21 (1923) 197–204; reprinted in P.A. MacMahon, Collected Papers, Vol. I, MIT Press, Cambridge, 1978, pp. 1090-1097.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Nathanson, M.B. N-graphs, Modular Sidon and Sum-Free Sets, and Partition Identities. The Ramanujan Journal 4, 59–67 (2000). https://doi.org/10.1023/A:1009830023023
Issue Date:
DOI: https://doi.org/10.1023/A:1009830023023