Skip to main content
SpringerLink
Log in

Three-dimensional numerical simulation of periodic natural convection in a differentially heated cubical enclosure

  • Regular Papers
  • Published:
Applied Scientific Research Aims and scope Submit manuscript

Abstract

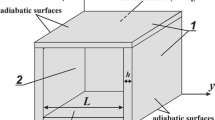
A high-resolution, finite-difference numerical study is carried out of three-dimensional unsteady periodic natural convection of air in a cubical enclosure at the Rayleigh number of 8.5×106. The enclosure is subjected to differential heating at the two vertical side walls. The other vertical walls are insulated. A linear temperature profile is specified at the thermally-conducting horizontal walls. Flow details in the three-dimensional field are captured by elaborate post-processing of the computational results, for which the state-of-the-art numerical visualization techniques are utilized. The three-dimensionality of the mean flow fields is observed to be confined into narrow regions near the end walls. The time-dependent solutions clearly indicate the periodic nature of the flow. The oscillation frequency is in close agreement with the previous experimental measurements reported in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

c p :

specific heat at constant pressure

Fr:

Froude number, u 20 /g*L 0

f ND :

normalized frequency, f*/N where f* is the dimensional frequency

g :

gravitational acceleration

k :

thermal conductivity

L 0 :

reference length (enclosure height)

N :

Brunt-Väisälä frequency, [g * β *(T H −T C )L 0]1/2

p :

pressure

p 0 :

reference pressure (hydrostatic pressure)

Pr:

Prandtl number, c * p μ*/k*

Ra:

Rayleigh number, g * β * c * p ρ *2 L 30 (T H −T C )/µ * k *

Re:

Reynolds number, ρ* 0 L 0 μ*

t :

time

T :

temperature

T 0 :

reference temperature, (T C +T H )/2

T C , T H :

cooled and heated side wall temperatures

u 0 :

reference velocity, [g * β * L 0(T H −T C )]1/2

u, v, w :

velocity components in the x, y and z directions

x, y, z :

Cartesian coordinates

β :

thermal expansion coefficient

δ :

overheat ratio, (T H −T C )/T 0

μ :

viscosity

ρ :

density

*:

dimensional quantities

References

  1. G. de Vahl Davis, Natural convection of air in a square cavity: a bench mark numerical solution. Int. J. Numer. Methods Fluids 3 (1983) 249–264.

    Google Scholar 

  2. N. C. Markatos and K. A. Pericleous, Laminar and turbulent natural convection in an enclosed cavity. Int. J. Heat Mass Transfer 27 (1984) 755–772.

    Google Scholar 

  3. H. Ozoe, A. Mouri, M. Ohmura, S. W. Churchill and N. Lior, Numerical calculations of laminar and turbulent natural convection in water in rectangular channels heated and cooled isothermally on the opposing vertical walls. Int. J. Heat Mass Transfer 28 (1985) 125–138.

    Google Scholar 

  4. P. Le Quere and T. Alziary de Roquefort, Transition to unsteady natural convection of air in differentially heated vertical cavities. In: Significant Questions in Buoyancy Affected Enclosure or Cavity Flows, ASME HTD-Vol. 60 (1986) pp. 29–36.

    Google Scholar 

  5. R. A. W. M. Henkes and C. J. Hoogendoorn, On the stability of the natural convection flow in a square cavity heated from the side. Appl. Sci. Res. 47 (1990) 195–220.

    Google Scholar 

  6. G. D. Mallinson and G. de Vahl Davis, Three-dimensional natural convection in a box: a numerical study. J. Fluid Mech. 83 (1977) 1–31.

    Google Scholar 

  7. A. M. Lankhorst and C. J. Hoodendoorn, Three-dimensional numerical calculations of high Rayleigh number natural convective flows in enclosed cavities. In: Proc. 1988 Nat. Heat Transfer Conf. ASME HTD-96, Vol. 3 (1988) pp. 463–470.

    Google Scholar 

  8. T. S. Lee, G. H. Son and J. S. Lee, Numerical predictions of three-dimensional natural convection in a box. In: Proc. 1st KSME-JSME Thermal and Fluids Engineering Conf. Vol. 2 (1988) pp. 278–283.

    Google Scholar 

  9. S. M. Bajorek and J. R. Lloyd, Experimental investigation of natural convection in partitioned enclosures. J. Heat Transfer 104 (1982) 527–532.

    Google Scholar 

  10. R. J. Krane and J. Jessee, Some detailed field measurements for a natural convection flow in a vertical square enclosure. In: Proc. 1st ASME-JSME Thermal Engineering Joint Conf. Vol. 1 (1983) pp. 323–329.

    Google Scholar 

  11. D. G. Briggs and D. N. Jones, Two-dimensional periodic natural convection in a rectangular enclosure of aspect ratio one. J. Heat Transfer 107 (1985) 850–854.

    Google Scholar 

  12. S. M. Bilski, J. R. Lloyd and K. T. Yang, An experimental investigation of the laminar natural convection velocity in square and partitioned enclosures. In: Proc. 8th Int. Heat Transfer Conf. Vol. 4 (1986) pp. 1513–1518.

    Google Scholar 

  13. D. N. Jones and D. G. Briggs, Periodic two-dimensional cavity flow: effect of linear horizontal thermal boundary condition. J. Heat Transfer 111 (1989) 86–91.

    Google Scholar 

  14. W. J. Hiller, S. Koch, T. A. Kowalewski, G. de Vahl Davis and M. Behnia: Experimental and numerical investigation of natural convection in a cube with two heated side walls. In: Proc. Int. Union Theoretical and Applied Mechanics Symp. (1990) pp. 717–726.

  15. K. H. Winters, Hopf bifurcation in the double-glazing problem with conducting boundaries. J. Heat Transfer 109 (1987) 894–898.

    Google Scholar 

  16. S. Paolucci and D. R. Chenoweth, Transition to chaos in a differentially heated vertical cavity. J. Fluid Mech. 201 (1989) 379–410.

    Google Scholar 

  17. S. V. Patankar, Numerical Heat Transfer and Fluid Flow: Hemisphere Publishing Corp. (1980) Chap. 6.

  18. H. L. Stone, Iterative solution of implicit approximations of multi-dimensional partial differential equations. J. Numer. Analy. 5 (1968) 530–558.

    Google Scholar 

  19. C. J. Freitas, R. L. Street, A. N. Findikakis and J. R. Koseff, Numerical simulation of three-dimensional flow in a cavity. Int. J. Numer. Methods Fluids 5 (1985) 561–575.

    Google Scholar 

  20. T. Fusegi, J. M. Hyun, K. Kuwahara and B. Farouk, A numerical study of 3-D natural convection in differentially heated cubical enclosure. Int. J. Heat Mass Transfer 34 (1991) 1543–1557.

    Google Scholar 

  21. S. Shirayama and K. Kuwahara: Patterns of three-dimensional boundary layer separation. 25th Aerospace Sciences Meeting (1987) AIAA Paper 87-0461.

Download references

Author information

Authors and Affiliations

  1. Institute of Computational Fluid Dynamics, 1-22-3 Haramachi, Meguro, 152, Tokyo, Japan

    Toru Fusegi

  2. Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, Chong Ryang, 131, Seoul, Korea

    Jae Min Hyun

  3. Institute of Space and Astronautical Science, 3-1-1 Yoshinodai, 229, Sagamihara, Kanagawa, Japan

    Kunio Kuwahara

Authors
  1. Toru Fusegi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jae Min Hyun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kunio Kuwahara
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fusegi, T., Hyun, J.M. & Kuwahara, K. Three-dimensional numerical simulation of periodic natural convection in a differentially heated cubical enclosure. Applied Scientific Research 49, 271–282 (1992). https://doi.org/10.1007/BF00384627

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00384627

Keywords

Search

Navigation