Skip to main content
SpringerLink
Log in

A theory for vortex shedding from the keels of marine vehicles

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Summary

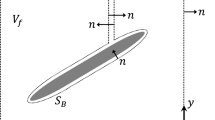
This paper presents a discrete vortex-shedding method for predicting the damping forces experienced by a floating marine vehicle responding at and around roll resonance. The method utilizes a Schwartz-Christoffel transformation, the temporal flow development being calculated to yield vortex positions, pressures and overall forces on the vessel hull. The effect of the velocity term in Bernoulli's equation on hull forces is calculated by integrating pressure and confirmed using the Blasius formula. A functional form of the vortex-induced moment amplitude is deduced from the theory and applied to a frequency-domain equation of roll motion for the vessel. Comparison of theory with test data indicates that the vortex-shedding theory does predict the effects of this phenomenon on the roll motions of a specific hull shape. An extensive review of previous work in this area is also presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. W. Froude, On, the resistance in rolling of ships, Naval Science 3 (1874) 312.

    Google Scholar 

  2. M. Martin, Roll damping due to bilge keels, Iowa Inst. of Hydraulic Research, Contract Nonr. 1611 (01), Nov. 1958.

  3. Sir, W. White, Notes on further experience with first class battleships, Trans. Inst. Nav. Arch. 36 (1895) 127.

    Google Scholar 

  4. G.H. Bryan, The action of bilge keels, Trans. Inst. Nav. Arch. 42 (1900) 198.

    Google Scholar 

  5. R.W.L. Gawn, Rolling experiments with ships and models in still water, Inst. Nav. Arch. 82 (1940).

  6. J.F. Dalzell, A note on the form of ship roll damping, J. Ship Research 22 (1978) 178–185.

    Google Scholar 

  7. H. Kato, On the frictional resistance to rolling of ships, Soc. Nav. Arch. Japan 102 (1958) 115.

    Google Scholar 

  8. N. Tanaka, A study on bilge keels (Pt. 4, On the eddy-making resistance to the rolling of a ship hull), Soc. Nav. Arch. Japan 109 (1960) 205–212.

    Google Scholar 

  9. N. Salvesen, E.O. Tuck and O. Faltinsen, Ship motions and sea loads, Trans. Soc. Nav. Arch. Marine Engrs. 78 (1970) 421.

    Google Scholar 

  10. Y. Ikeda, Y. Himeno and N. Tanaka, A prediction method for ship roll damping, Dept. of Nav. Arch., Univ. of Osaka, Japan, Rep. 00405 (1978).

  11. J.N. Newman, Marine hydrodynamics, MIT Press, 2nd edn. (1978).

  12. Y. Ikeda, Y. Himeno and N. Tanaka, On eddy making component of roll damping force on naked hull, J. Soc. Nav. Arch. Japan 142 (1977) 54.

    Google Scholar 

  13. J.A. Kcuning and W. Beukelman, Hydrodynamic coefficients of rectangular barges in shallow water, Paper 55, BOSS'79, Imperial Coll. Sci. Tech. London (1979) 105–124.

  14. W.P. Stewart, W.A. Ewers and P.J. Denton, Nonlinear barge motion response. Use of physical models in the design of offshore structures, Paper 23, Garston, Watford, England (1979).

  15. P. Kaplan, C.W. Jiang and J. Bentson, Hydrodynamic analysis of barge-platform systems in waves. RINA Spring Meeting, Paper 8, (1982).

  16. J.-P.F. Denise, On the roll motion of barges, RINA Supplementary Paper 125 (1983) 255.

    Google Scholar 

  17. D.T. Brown, R. Eatock Taylor and M.H. Patel, Barge motions in random seas-a comparison of theory and experiment, J. Fluid Mech. 129 (1983) 385–407.

    Google Scholar 

  18. L. Rosenhead, Formulation of vortices from a surface of discontinuity, Proc. Roy. Soc. 134 (1931) 170–192.

    Google Scholar 

  19. G.D. Birkhoff and J. Fisher, Do vortex sheets roll up?, Rendi. Circ. Math. Palermo 8 (1959) 1077.

    Google Scholar 

  20. F.R. Hama and E.R. Burke, On the rolling up of a vortex sheet, Univ. of Maryland Tech. Note BN-220, USA (1960).

  21. F.H. Abernathy and R.E. Kronauer, The formation of vortex streets, J. Fluid Mech. 13 (1962) 1–20.

    Google Scholar 

  22. F.L. Westwater, The rolling up of the surface of discontinuity behind an aerofoil of finite span, R. and M. 1692, Aero. Research Council, GB (1935).

    Google Scholar 

  23. H. Kaden, Aufwicklung einer unstabilen Unstetigkeitsflache, Ing. Arch. 2 (1931) 140–168.

    Google Scholar 

  24. D.W. Moore, The discrete vortex approximation of a finite vortex sheet, Cal. Inst. Tech. Rep., AFOSR, USA (1971) 1804–1869.

    Google Scholar 

  25. R.R. Clements, An inviscid model of two-dimensional vortex shedding, J. Fluid Mech. 57 (1973) 321–336.

    Google Scholar 

  26. R.R. Clements and D.J. Maull, The representation of sheets of vorticity by discrete vortices, Prog. Aerospace Sci. 16 (1975) 129–146.

    Google Scholar 

  27. K. Kuwahara, Numerical study of flow past an inclined flat plate by an inviscid model, J. Phys. Soc. Japan 35 (1973) 1545–1551.

    Google Scholar 

  28. T. Sarpkaya, Inviscid model of two-dimensional vortex shedding for transient and asymptotically steady separated flow over an inclined plate, J. Fluid Mech. 68 (1975) 109–128.

    Google Scholar 

  29. L.M. Milne-Thomson, Theoretical hydrodynamics, Macmillan & Co., 5th edn., (1968).

  30. P.T. Fink and W.K. Soh, Calculation of vortex sheets in unsteady flow and applications in ship hydrodynamics, Proc. 10th Symp. Naval Hydrodynamics, Cambridge, Massachusetts, USA, (1974) 463–491.

  31. P.K. Stansby, An inviscid model of vortex shedding from a circular cylinder in steady and oscillatory far flows, Proc. Inst. Civ. Engrs. 63 (1977) 865–880.

    Google Scholar 

  32. T. Sarpkaya and R.L. Schoaff, Inviscid model of two-dimensional vortex shedding by a circular cylinder, AIAA J. 17 (1979) 1193.

    Google Scholar 

  33. M. Efthymiou and R. Narayanan, Current induced forces on submarine pipelines-a discrete vortex model, Proc. Inst. Civ. Engrs. 73 (1982) 109–123.

    Google Scholar 

  34. M.H. Longuet Higgins Oscillating flow over steep sand ripples, J. fluid Mech. 107 (1981) 1–35.

    Google Scholar 

  35. P.W. Bearman, J.M.R. Graham, P. Naylor and E.D. Obasaju, The role of vortices in oscillatory flow bluff cylinders, Proc. Int. Symp. Hydrodynamics in Ocean Engng., NIT Trondheim, Norway (1981).

    Google Scholar 

  36. J.M.R. Graham, The forces on sharp edged cylinders in oscillatory flow at low Keulegan-Carpenter numbers, J. Fluid Mech. 97 (1980) 331–346.

    Google Scholar 

  37. P.W. Bearman, M.H. Downie and J.M.R. Graham, Calculation method for separated flows with application to oscillatory flow past cylinders and roll damping of barges, Unpublished report, Imperical Coll. Sci. Tech. London (1983).

    Google Scholar 

  38. O.M. Faltinsen and B. Pettersen, Vortex shedding around two-dimensional bodies at high Reynolds number Proc. 14th Symp. on Naval Hydrodynamics, Univ. of Michigan, Ann Arbor, USA, (1982).

    Google Scholar 

  39. A. Pope, Basic wing and airfoil theory, McGraw-Hill Book Comp., New York, Ist edn. (1951).

    Google Scholar 

  40. L. Landweber and C.S. Yih, Forces, moments and added masses for Rankine bodies, J. Fluid mech. 1 (1956) 319–336.

    Google Scholar 

  41. P.K. Stansby, A numerical study of vortex shedding for one or two cylinders, Proc. European Mech. Colloq., London, No. 119, 1979.

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University College London, Torrington Place, WC1E 7JE, London, England

    D. T. Brown & M. H. Patel

Authors
  1. D. T. Brown
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. H. Patel
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Brown, D.T., Patel, M.H. A theory for vortex shedding from the keels of marine vehicles. J Eng Math 19, 265–295 (1985). https://doi.org/10.1007/BF00042874

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00042874

Keywords

Search

Navigation