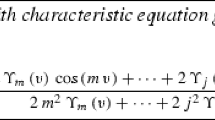Abstract
The method of finite differences is applied to the solution of the two-dimensional time-dependent Schrödinger equation. The equidistant mesh is used and the accuracy of the formulae approximating the kinetic energy term by polynomials of the 2nd, 4th and 6th order in the mesh size is discussed. The numerical results are compared to the exact solutions corresponding to the square well potential.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Flocard, H., Koonin, S.E., Weiss, M.S.: Phys. Rev. C17, 1682 (1978)
Koonin, S.E.: Phys. Lett.61B, 227 (1976)
Koonin, S.E., Davies, K.T.R., Maruhn-Rezwani, V., Feldmeier, H., Krieger, S.J., Negele, J.W.: Phys. Rev. C15, 1359 (1977)
Varga, R.S.: Matrix Iterative Analysis. Englewood Cliffs, New Jersey: Prentice Hall 1962
Nakamura, S.: Computational Methods in Engineering and Science. New York: Wiley 1978
Jennings, A.: Matrix Computation for Engineers and Scientists. New York: Wiley 1978
Author information
Authors and Affiliations
Additional information
The author would like to express his gratitude to Professor H.C. Pauli for helpful discussions and valuable comments. He also wishes to thank Professor H.A. Weidenmüller for his kind interest in the work and for reading the manuscript.
Rights and permissions
About this article
Cite this article
Dudek, J. Comment on the finite difference schemes for the time-dependent Schrödinger equation. Z Physik A 292, 205–210 (1979). https://doi.org/10.1007/BF01441627
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01441627