Simulation of geological surfaces using fractals

Abstract

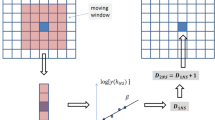
Methods suggested in the past for simulated ore concentration or pollution concentration over an area of interest, subject to the condition that the simulated surface is passing through specifying points, are based on the assumption of normality. A new method is introduced here which is a generalization of the subdivision method used in fractals. This method is based on the construction of a fractal plane-to-line functionf(x, y, R, e, u), where(x, y) is in[a, b]×[c, d], R is the autocorrelation function,e is the resolution limit, andu is a random real function on [−1, 1]. The simulation using fractals escapes from any distribution assumptions of the data. The given network of points is connected to form quadrilaterals; each one of the quadrilaterals is split based on ways which are extensions of the well-known subdivision method. The quadrilaterals continue to split and grow until resolution obtained in bothx andy directions is smaller than a prespecified resolution. If thex coordinate of theith quadrilateral is in[a _i ,b _i ] and they coordinate is in[c _i ,d _i ], the growth of this quadrilateral is a function of(b _i −a _i ) and(d _i −c _i ); the quadrilateral could grow toward the positive or negativez axis with equal probability forming four new quadrilaterals having a common vertex.